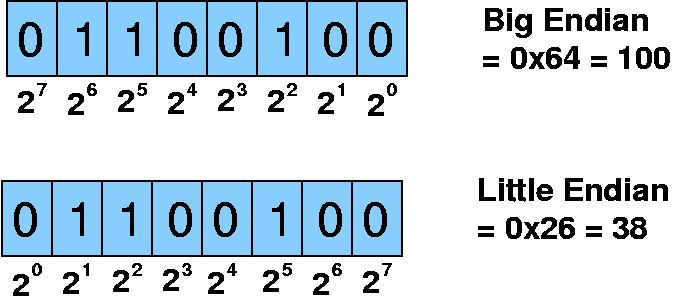CDA-4101 Lecture 4 Notes
Memory
Memory - where programs and data are stored
|
- Primary Memory - fast, volatile (this lecture)
- Secondary Memory - slower, larger, permanent (next lecture)
| 
|
Bits
- Bit - smallest storage unit, binary valued
Q: Why are bits binary?
A: reliability
Recent Memory News
|
Recent news story about atomic level memories:
(Himpsel, et. al., U. Wiscosin, Madison, 9/3/2002)
- small channels where there either is or is not an atom
- requires expensive scanning/tunnelling microscope equipment
- provides a storage density a million times greater than a
CD-ROM, today's conventional means of storing data.
- Similar to the way DNA encodes information (moleculoar level).
|
Encoding

|
- we have bits in the hardware, but letters, numbers, words, shapes,
concepts and ideas are our world's data that need to be stored.
- language itself is an encoding, where the alphabet is the
"hardware" we can encode our ideas in.
- Just like learning a new language, computer scientists/engineers
need to learn a new encoding and map it back to a more natural
representation.
|
Complications
- engineers have differed over the binary encoding language
- BCD (binary coded decimal) vs. pure binary
- pure binary "more efficient" for integers
- floating point numbers even more complex, which we will see later
in the course
- ASCII/EBCDIC for representing characters
- for representing more than these simple ideas: data structures
ASCII Codes
EBCDIC Codes
Octal and Hexadecimal
- shorthands for binary representations
- octal - group of 3 bits
- hexadecimal - group of 8 bits (two groups of 4)
Memory Layout
- cells/locations
- addresses
- memory size defined by cell size and number of cells
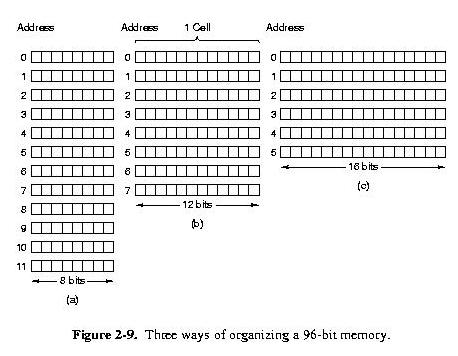
- addressing starts at 0
- all cells same number of bits
- a cell with n-bits can hold 2^n different bit combinations
- 8-bit (byte) cell is standard
Addresses

|
- also represented in binary
- number of addressable memory locations defines how many bits are
needed to represent all addresses
e.g., a 32 bit machine, usually means addresses limited to 32
bits, so it can address 232 distinct memory
addresses
|
Words
- most instructions operate at the word level
- registers accomodate words (not necessarily cells)
Little-endian vs. Big endian
Conflict: where is most significant bit/byte?
- hardware design decision (little endian = less circuits)
- book's figures can be confusing
- "rightmost and leftmost" is fabrication at byte-level
- bit ordering for bytes
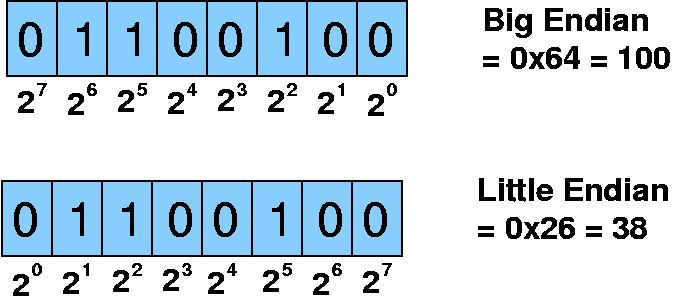
- important for transfers of one bit at a time (bit streams)
- mostly big-endian
Endian-ness for words
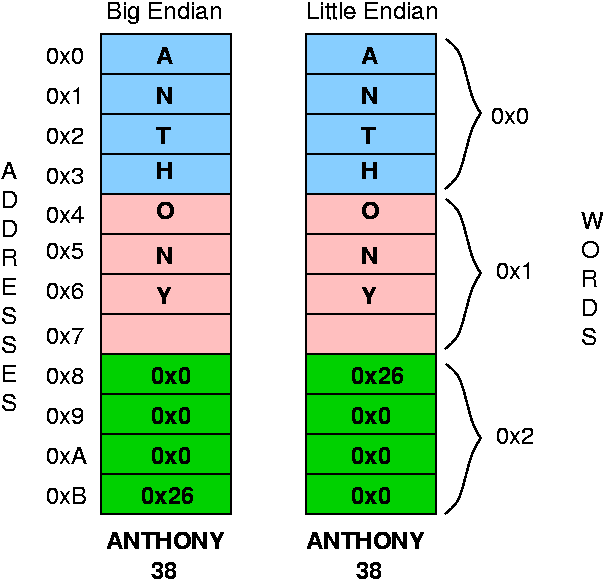
Transfer: Big endian to Little Endian
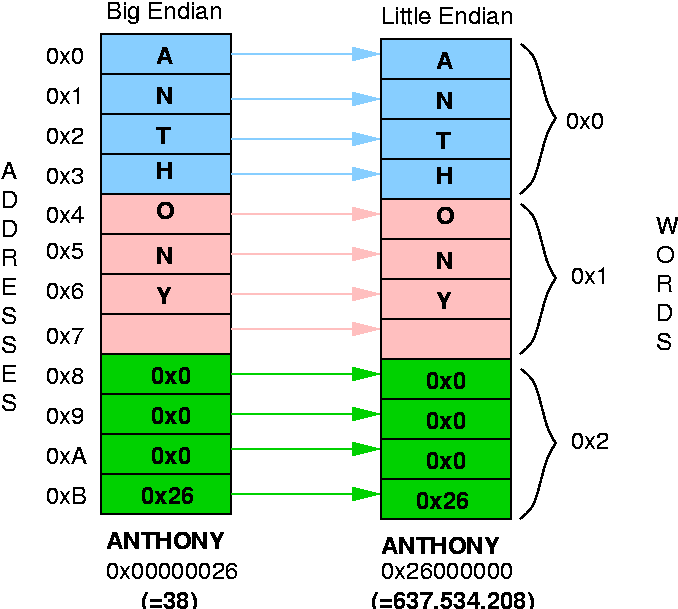
Transfer and Swap: Big endian to Little Endian
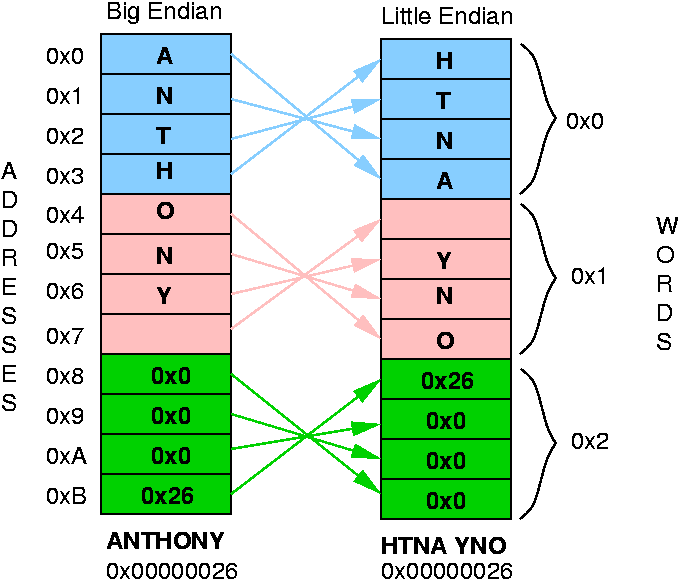
Real Machine Endian-ness
| Big-endian: | Little Endian | Both
|
IBM mainframes
Motorola processors (i.e., MACs)
| IBM PCs/clones
| Power-PC
|
Error-Correcting Codes
- needed due to voltage spikes/dips (mechanical )
- add extra bits to help detect errors
- e.g., my phone bill account number
- m data bits, r check bits, n = m + r = "codeword"
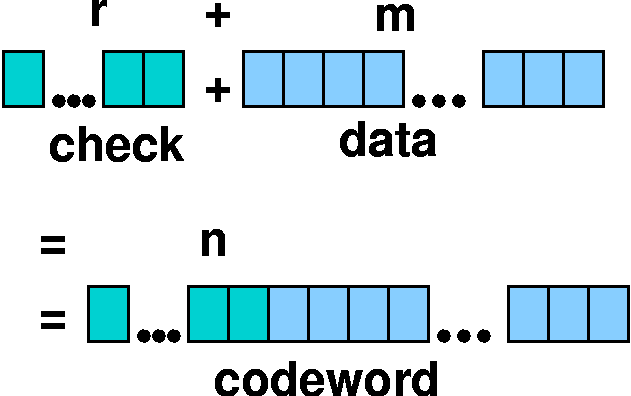
Hamming Distance
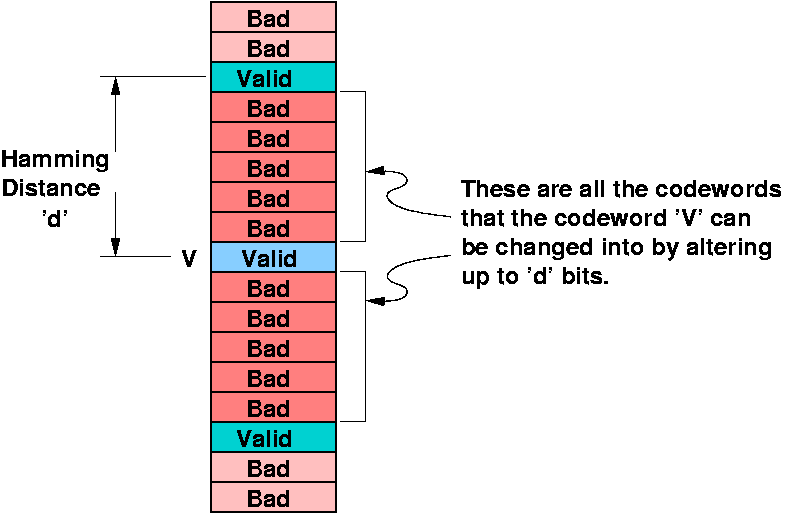
- bitwise XOR, then add all '1's
- measure how far apart two words are (number of errors that must
have occurred)
- In memory cells all 2m bit patterns are legal
- In codewords, only 2m of the 2n possible
patterns are legal, (since each 2m pattern has a single
unique setting for the other r check bits )
- Since there are many more possible patterns than legal patterns,
for a given codeword you can figure out if it is legal (error
detection) and sometimes which is the closest legal
codeword (error correction)
Hamming Distance for Detection
Hamming Example
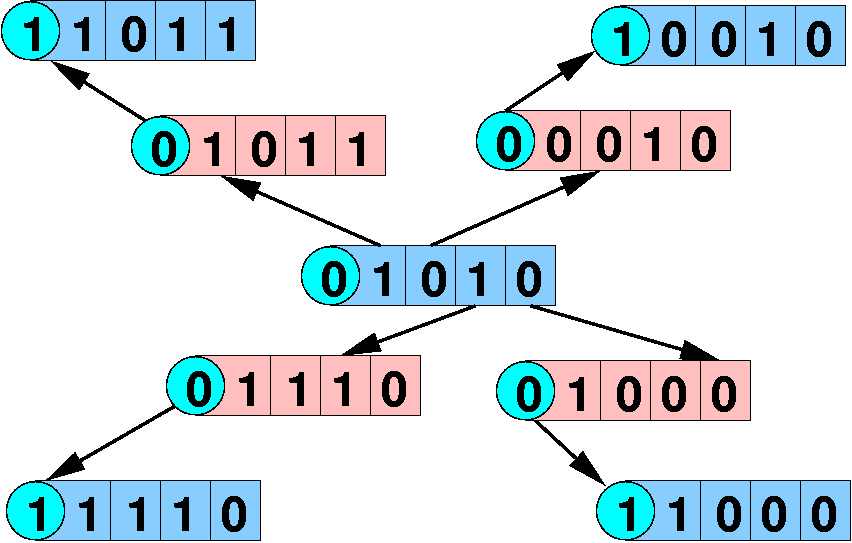
Hamming Example (cont)
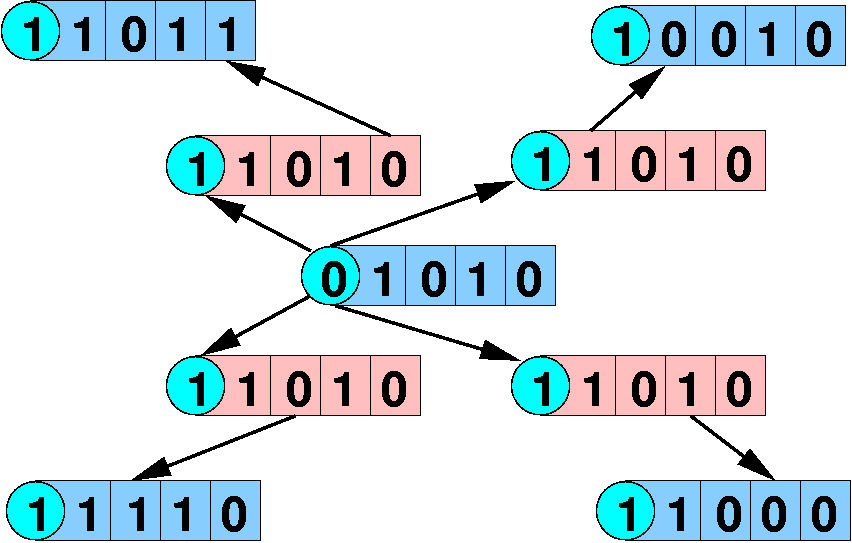
Hamming Distance for Correction
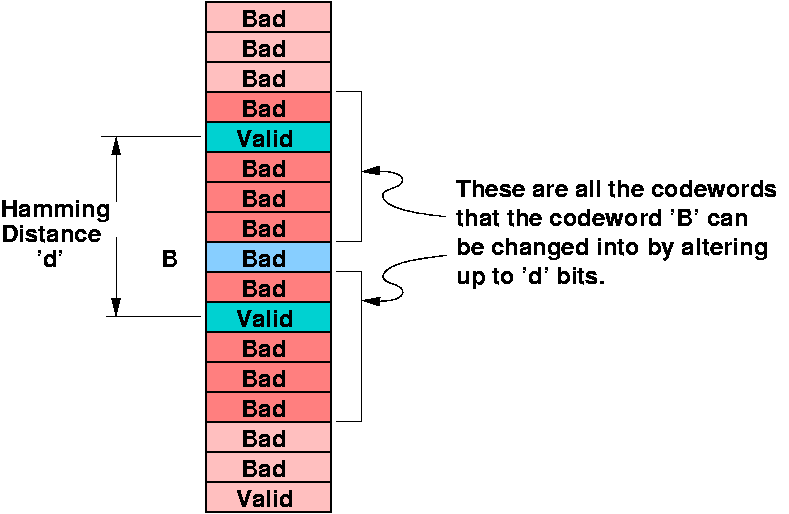
- Thus, you need a Hamming Distance of 2d + 1 to be able to do
error correction.
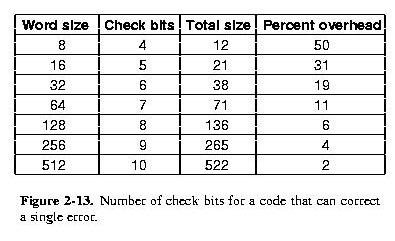
How many Check Bits?
- Correcting one-bit errors, needs a Hamming code with distance 3.
- 2m legal codewords, which have 'n' illegal code
words that are one bit off
- These 'n' illegals cannot be 1 bit from another legal code word or
the two legals would only be Hamming distance 2 apart.
- each 2m legal codewords need (n+1) total codewords
- there are a total of 2n possible codewords
Therefore the number of extra bits is bounded by:
| (n+1) 2m | <= | 2n
|
| (m+r+1) 2m | <= | 2(m+r)
|
| (m+r+1) 2m | <= | 2m 2r
|
| (m+r+1) | <=
| 2r
|
Table of Lower Bounds
Hamming Codes
- The previous algebra and table puts a lowerbound on the number of
bits, but it doesn't say if the lower bound is achievable.
- Mr. Hamming came up with an algorithm for achieving this limit
- Idea behind the algorithm:
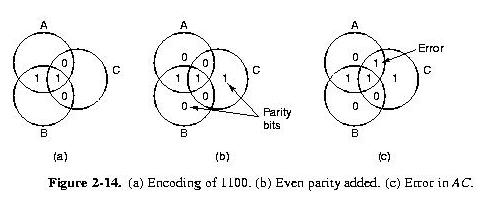
Read the details of the algorithm and understand it; there is a
homework problem about it.
Cache Memory

Cash!
|
- memory is typically small and fast, or large and slow
- caching is a way to use these two type of memory to get the effect
of a fast large memory.
- larger, cheaper RAM is much slower than the CPUs speeds
- memories can be built faster, but more expensive.
|
Principle of Locality
- data not acccessed at random (typically)
- programs sequence not random (sequential, loops)
- when data is used, keep it around "cache it", since it is
likely to be used again.
- also request for one piece of data bring in all data in vicinity
assuming these will soon be used
Cache Issues
- Success of Caching depends on the "hit rate": how frequently requested
data is found in the cache.
- Memories have propery that first access is slow, but subsequent
accesses are faster, thus allowing "blocks" of data to be transfered
more faster than if individually accessed.
Cache: Logical Location
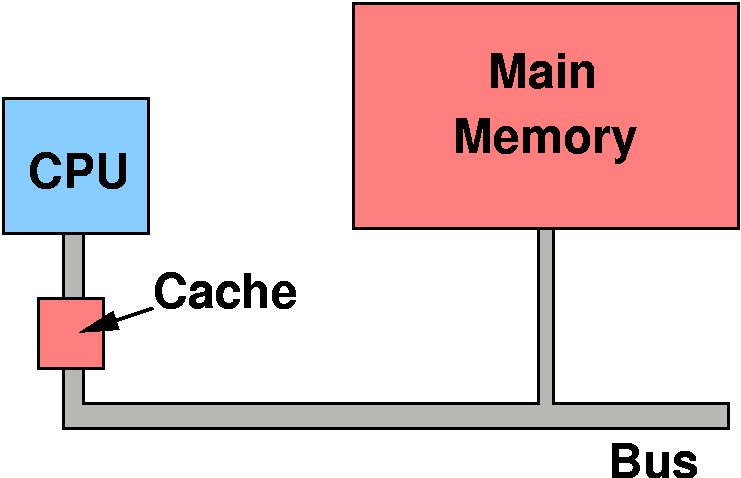
Cache Math
n = number of memory accesses
f = number found in cache
c = cache access time
m = memory access time
- hit ratio
h = f/n
- miss ratio
1 - h
- mean access time
c + (1-h)m
(always incur time 'c' since have to find out it is a miss)
- starting memory access at same time as cache access can speed it
up, but is more complicated
Cache Design Issues
- "cache line" size: block of data stored/transfered
- number of cache lines
- organization: bookkeeping, mapping memory addresses to cache
locations
Multiple caches
- reapplying caching principle
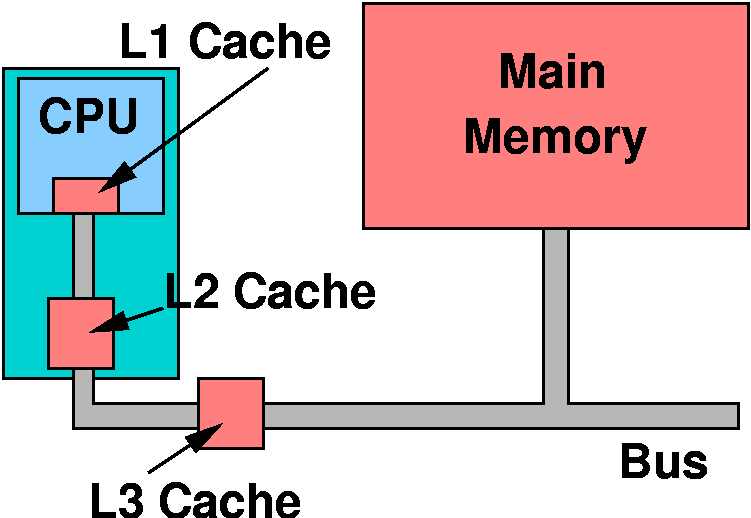
- unified cache (instructions and data)
- split cache
- helps pipeling, simultaneous IF and OF
- never have to write back cache results
Memory packaging
- Pre 1990's memory was individual chips put into the motherboard
- Post 1990's group of chips mounted on a printed circuit board with
some controlling chips and sold as a package.
- SIMMs single, in-line memory module (pins on one side)
- DIMMs dual inline memory module (pins on two sides)
- SIMM history
- 30 connectors, 8 data, rest contrrol and addressing
- 72 connectors, 32 data
- paired 72 pin SIMMs for Pentium to get 64 data bits at a time
- DIMMs current package type
- 84 connectors on each side (168 total), 64 data bits
SO-DIMM
Small Outline - for laptops