CDA-4101 Lecture 7 Notes
Digital Logic Level
- Basic simple digital elements
- How to combine these elements to do more useful things
- some mathematucal techniques for analyzing the combinations
- we start with "gates"
| 
|
Gates?

Gates?

Gates
- a "gate" is a small electronic device that performs a simple
electrical function
- gates are made from one or more transitors
- we will show how gates can be combined to do more complex
functions
Device Level (briefly)
- physical properties of semiconductors and clever arrangements of
them yield the basic functionality of a transitor.
- bipolar transitor (NPN), three connections to the outside
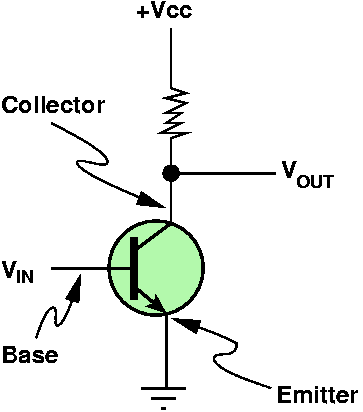
- When Vin drops below a certain critical voltage (low), transitor
turns "off" and its resistance is infinite
- the electrical flow will then go from +Vcc to Vout (path of least
resistance)
- when Vin is high enough, the transition turns on and will conduct
electricity
- electrical flow will then go from +Vcc to ground leaving Vout
with low or nearly no voltage
- Thus, Vout is always the inverse of Vin, and we have an
"inverter": if Vin is low, then Vout is high, if Vin is high, then
Vout is low
- This inversion can happen very fast (from a few nanoseconds to even
less)
- note that the resistor is used to prevent the transitor from burning
out
Two Transistors
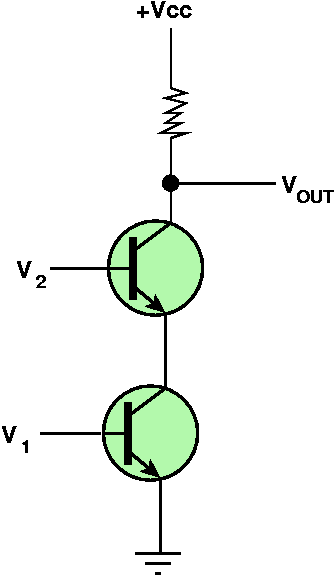
- In order for Vcc to want to go to ground, it will require both
transistors to be "on", i.e., V1 and V2 both set high
- If either V1 or V2 is low then Vout will be high
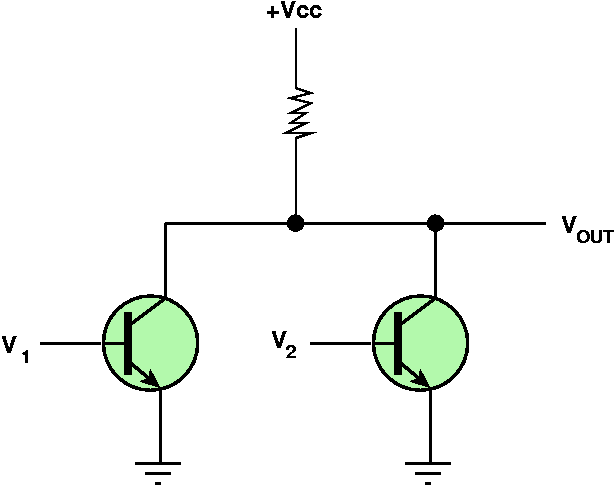
- Here, +Vcc will go to ground and Vout will be low if
either V1 or V2 is set to high
- Thus, to get a high value on Vout it needs both V1
and V2 to be low
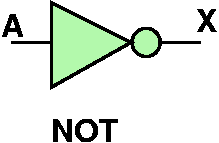
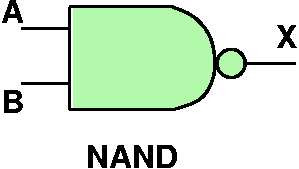
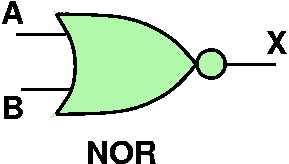
Gates
- These three transistor arrangements are the simplest three gates
- Because there is essentially two values "low" and "high", we can
assign these to logical 0 and logical 1 respectively
- We can also create a table that defines the entire circuit's logical
behavior

| 
| 
|
| 
| 
|
|
|
| A | B | X |
|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
|
| A | B | X |
|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
|
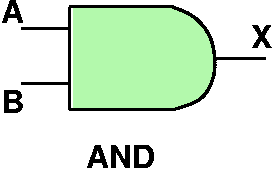
Two More Gates?

Two More Gates
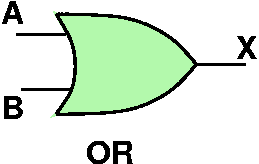
- The AND and OR logical functions have corresponding gates as
well.
- You can produce these by inverting the output of the NAND
and NOR gates respectively
| 
|
| A | B | X |
|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
|
| A | B | X |
|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
|
- Note that although these are the more common logical operators,
they actually require more transitors than the NAND and NOR
gates.
- Also, although the symbols for NAND and NOR explicitly show the
inversion bubbles, it is the AND and the OR gates that
will need the additional inverter transistor
- All of these gates can be made to have more than two inputs.
Boolean Algebra
- an algebra is any system of properties and relationshsips
- algebra, as you probably know it, is actually just the algebra
of the real numbers
- there are many other mathematical systems, each with their own
algebra
- in a digital world with only two values, we will need to study
and use boolean algebra
- technically, we will be using a switching algebra which
is very closely related to boolean algebra, but we will not worry
about this difference
| 
|
Boolean Functions
- with real numbers, functions can have ranges and domains that span an
(uncountably) infinite set of numbers.
- boolean functions are restricted to ranges and domains from the set
{ 0, 1 }
- Example: The NOT function 'f':
f(0) = 1
f(1) = 0
- Example: The AND function 'g':
g(0,0) = 0
g(0,1) = 0
g(1,0) = 0
g(1,1) = 1
| 
George Boole
|
- we can use variables just like the familiar algebra,
though these take on only one of two values
- a variable can represent the voltage on the wire: high or low
- notice that because a function of 'n' variables has a finite
number of possible combinations, we can enumerate them all
- a truth table is a tabular way to specify a boolean
functions, e.g.,
|
|
| A | B | g(A, B) |
|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
|
Larger Boolean Functions
| A | B | C | M |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
|
|
|
Implementing Boolean Functions
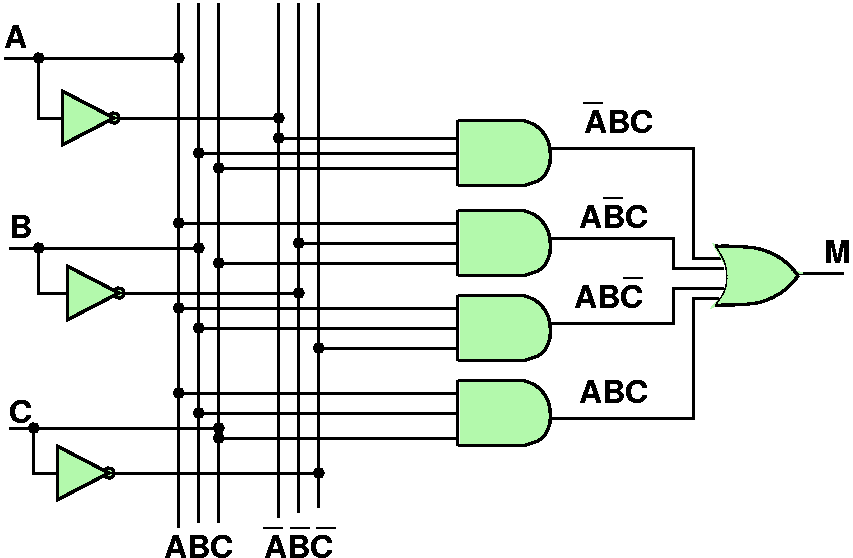
- Note that "dots" indicated where crossing lines are
connected.
Complete Gates
- we've seen that NAND and NOR require less transitors
- also, it is sometimes more convenient to use only a single type
of gate
- any circuit can be converted into a form that uses only NAND or
only NOR gates
- a single gate type that can implement any boolean function is
called a complete gate
- NAND and NOR are the only complete gates
- note that the set of NOT, AND and OR gates together can also
form any boolean function
|

"In high school I took a little English, some science, some
hubcaps and some wheel covers." - William James "Gates" Brown
|

NAND Completeness
|
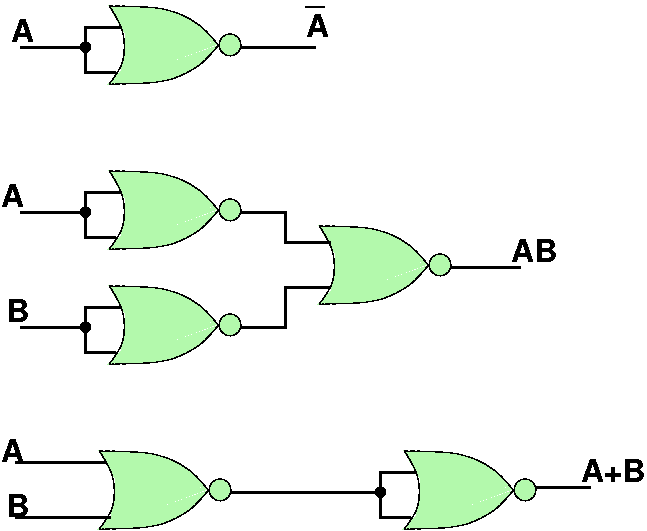
NOR Completeness
|
Circuit Equivalence
- The straightforward implementation is not always the best
- conversion to only NANDs or NORs or reduction of the total
number of gates will be cheaper, simpler and faster
- we need some techniques for taking arbitrary boolean functions
and finding a logically equivalent, but differnt boolean
function that uses fewer and/or different types of gates.
- we'll look at two techniques for finding simpler circuits:
- Boolean algebra
- Karnaugh Maps (not in the textbook)
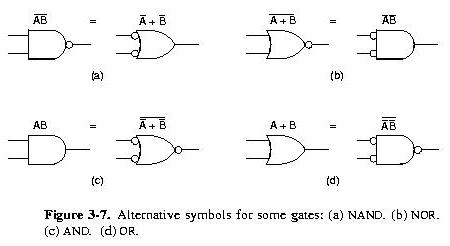
Boolean Algebra Identities
- You can prove these identities by constructing their truth
tables (this is a perfectly valid "proof")
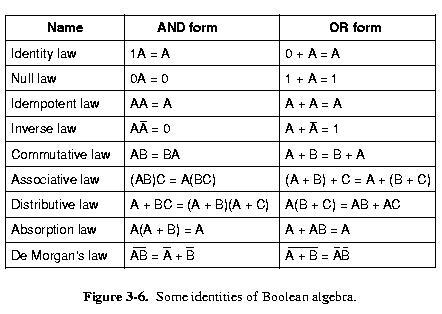
Circuit Reduction Using Boolean Algebra
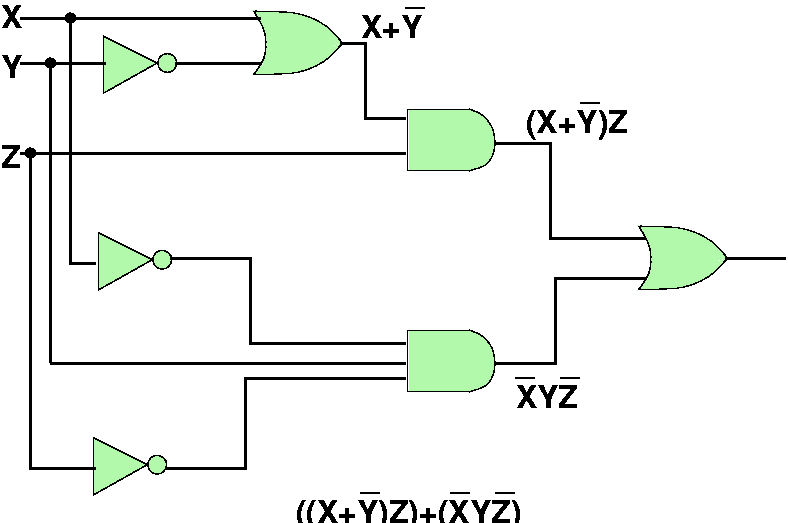
Original Circuit
Circuit Reduction I
Reduction:
F(X,Y,Z) = ((X + Y')Z) + (X'YZ')
= XZ + Y'Z + X'YZ' (distribute)
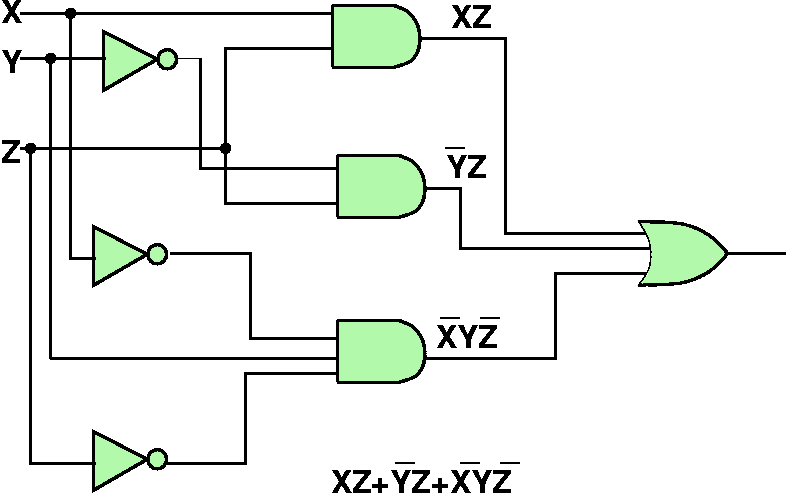
Equivalent Circuit
- There are less "levels" in the equivalent circuit, so there will
be less latency time for the signals to propogate
Circuit Reduction II
Identity:
(AB) + (CD) = (A+C)(A+D)(B+C)(B+D) ("adding out")
Follows from:
(AB) + (CD) = (AB + C)(AB + D) (distributive law)
(AB) + (CD) = ((A+C)(B+C))((A+D)(B+D)) (distributive law)
Generalizes to:
(X1 X2 ... Xn) + (Y1 Y2 ... Yn)
= (X1+Y1)(X1+Y2)...(X1+Yn)(X2+Y1)(X2+Y2)...(Xn+Y1)...(Xn+Yn)
Another Reduction:
F(X,Y,Z) = ((X + Y')Z) + (X'YZ')
= (X + Y' + X')(X + Y' + Y)(X + Y' + Z')(Z + X')(Z + Y)(Z + Z')
= 1 1 (X + Y' + Z')(Z + X')(Z + Y) 1
= (X + Y' + Z')(Z + X')(Z + Y)
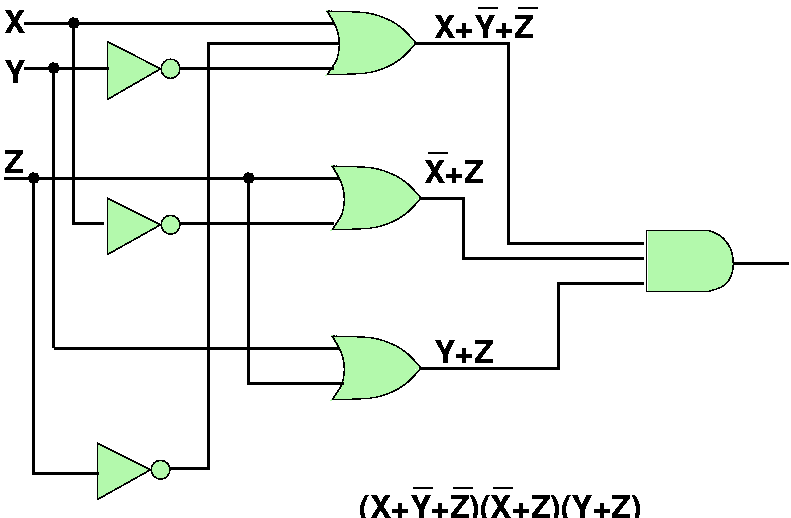
Another Equivalent Circuit
Karnaugh Maps
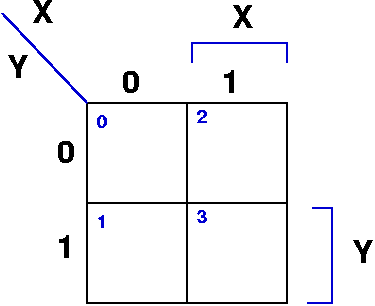
Karnaugh Map of 2 Variables
|
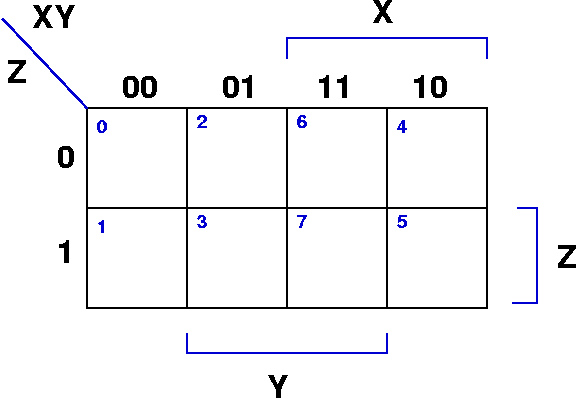
Karnaugh Map of 3 Variables
|
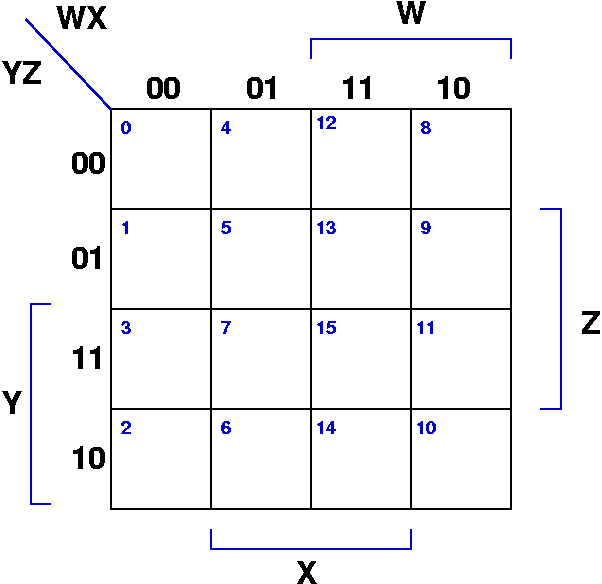
Karnaugh Map of 4 Variables
|
- a graphical representation of a logic function's truth
table
- small number in boxes is the row of the truth table (assuming
truth table ordered by their binary number equivalents)
- boxes are filled in with the function's value from that row of
the truth table.
- the non-sequential ordering of the varibale values in the rows
and columns is very important: it ensures that adjacent cells
differ by only one bit
- adjacency of cells "wraps around" on both the left/right and
top/bottom
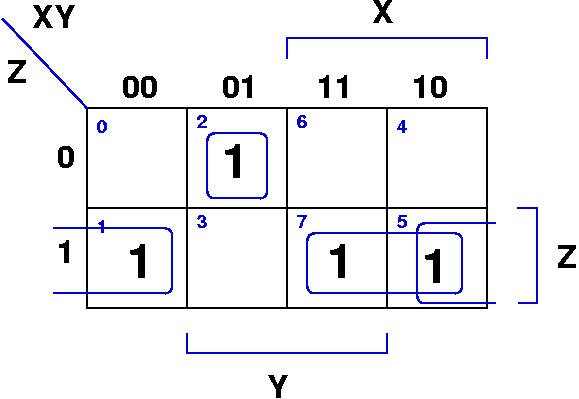
Karnaugh Map Example
| X | Y | Z | F(X,Y,Z) |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
|
F(X,Y,Z) = X'Y'Z + X'YZ' + XY'Z + XYZ
- note that each '1' in the box represents one of the
product terms in a sum of products representation for the
function
- we can reduce clutter in the map by only writing the 1's
and assuming empty cells are zeroes
|
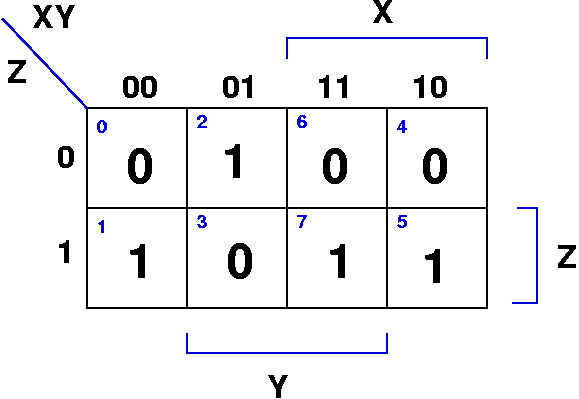
|
Karnaugh Map Example (cont.)
Karnaugh Map Example (cont.)
Karnaugh Map Procedure
- Fill in the Karnaugh map from the truth table or any other
representation of the function.
- group 1's that are adjacent and make the groupings as
large as possible
- dimensions of resulting groupings must be rectangles whose
dimensions are powers of two (e.g., 1x1, 1x2, 1x4, 2x4, 4x4, etc.)
- ensure all 1's are contained in at least one grouping, though note that
they can appear in more than one grouping
- if within the grouping a variable always has value 1, then the
variable will appear in the product term.
- if within the grouping a variable always has value 0, then the
complement of that variable will appear in the product term.
- if within the grouping a variable take on both 0 and 1 values,
then that variable will not appear in the product term
- add (OR) all the product terms from each grouping together
Bigger Karnaugh Map Example
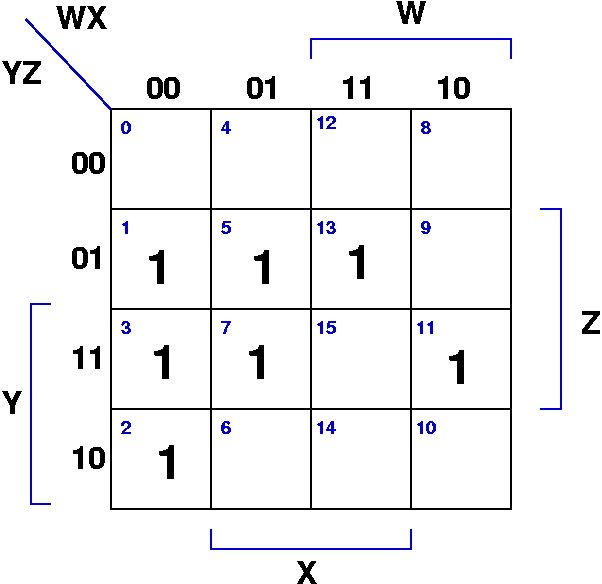
Prime Number Detector
- Prime numbers from 0 to 15 are: 1, 2, 3, 5, 7, 11, 13
-
F(W,X,Y,Z) = W'X'Y'Z + W'X'YZ' + W'X'YZ + W'XY'Z + W'XYZ + WX'YZ + WXY'Z
|
|
Bigger Karnaugh Map Example (cont.)
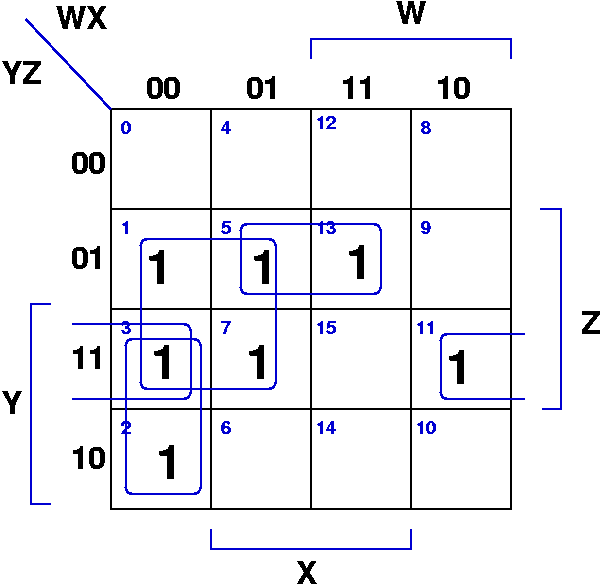
Prime Number Detector
- there are 4 groupings
- F(W,X,Y,Z) = W'Z + XY'Z + X'YZ + W'X'Y
|
|
Karnaugh Maps and Duality
- You can focus on the zeroes of a Karnaugh map instead of the
ones.
- You just have to make sure that you complement the results you
get.
- don't worry about doing this though
What if We "Don't Care"?
- Often in digital design, there are combinations of input that we
might know are impossible or that we really just don't care
about what value the function takes for these inputs
- we can exploit this knowledge in Karnaugh maps to help us get a
minimal boolean function
"Don't Care" Karnaugh Map Example
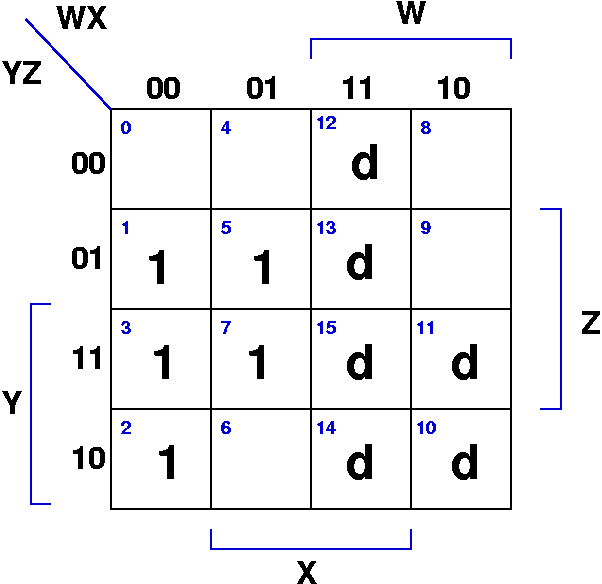
BCD Prime Number Detector
- with a BCD representation, the values 10 through 15 aree not
possible, so the primes are: 1, 2, 3, 5, 7
- we don't care whether the function is 1 or 0 for any values
greater than 9
- F(W,X,Y,Z) = W'X'Y'Z + W'X'YZ' + W'X'YZ + W'XY'Z + W'XYZ
|
|
"Don't Care" Karnaugh Map Example (cont.)
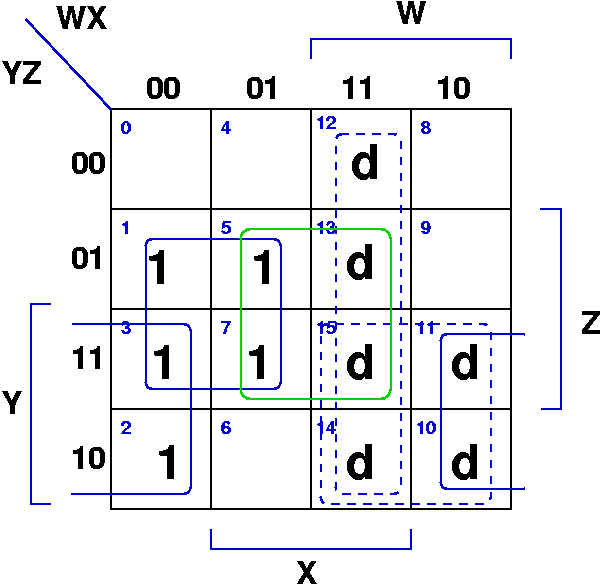
BCD Prime Number Detector
- we have choices about which groupings to take
- groupings containing only "don't cares" shouldn't be included
- just ensure that set of groupings selected "cover" all 1's
- F(W,X,Y,Z) = W'Z + X'Y
|
|